课件
所谓元素选择问题,就是找出一个(无序)序列 xs 中第 n 小的元素。
select :: Ord a => Int -> [a] -> a
堆排序算法可以先找出一组数的最大值,再找次大值,这样一个个地排序;所以可以用于选择问题。它所做的就是在线性序集上应用完全二叉树的拓扑结构,来优化元素“上浮”的路径到最短。
代码:
一些例子:
❯ ghci
GHCi, version 8.6.5: http://www.haskell.org/ghc/ :? for help
Prelude> :load heap.hs
[1 of 1] Compiling Main ( heap.hs, interpreted )
Ok, one module loaded.
*Main> heapselect 3 [1,2,3,4,5,6,7,8,9]
3
*Main> heapselect 9 [51,75,45,41,71,28,32,2,91,41]
75
到这里都是一堂平常算法课的内容。通常,接下来应该考察一下算法的时间复杂度了。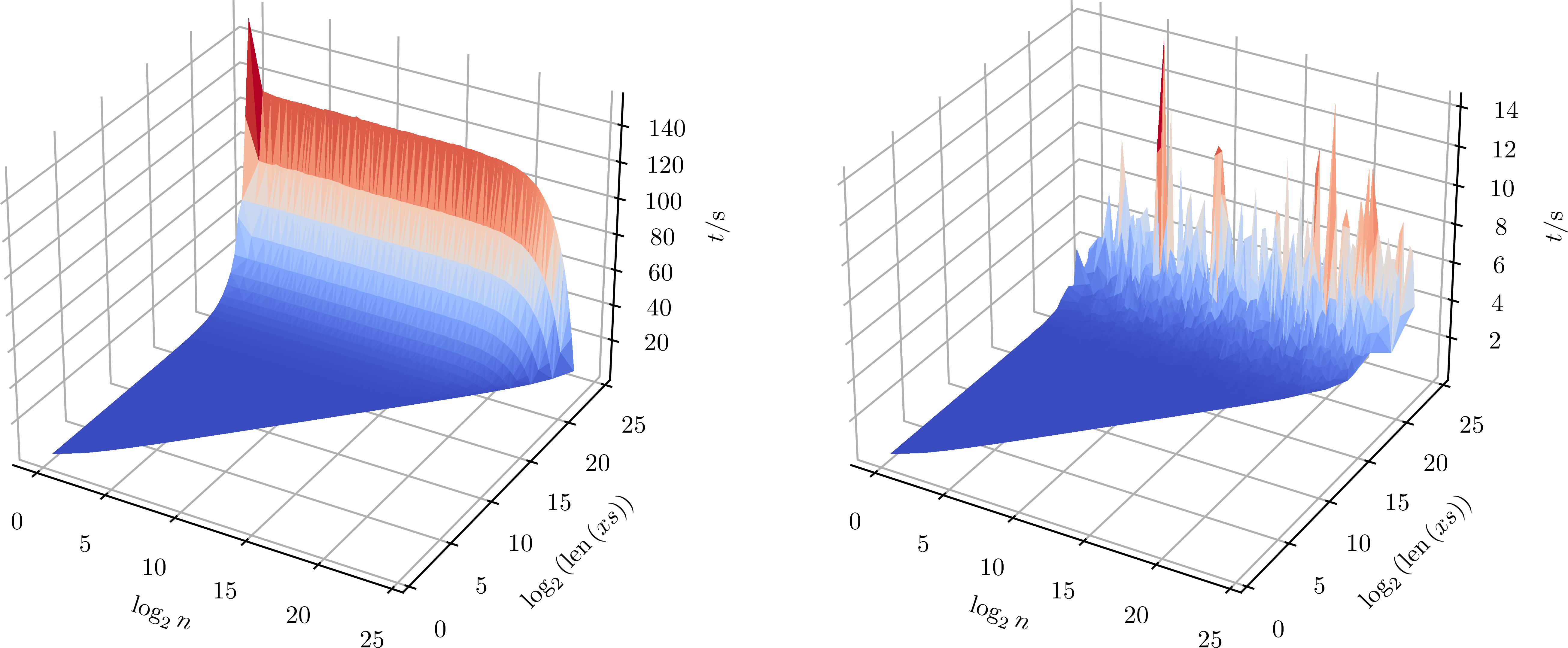
算法在 Python 3.8.5 上实现。
正是在这里,我们的课件中出现了一个直到结课都没人指出的错误。在我们没有教学的教学环境中,这只是一个平常时刻。
起码不能说,改正这里的错误不是一件重要的事。人是会思考的存在,而这里只不过是没有思考,只有存在而已。在我们没有无穷的无穷生命中,这只是一个平常时刻。
对于未知的知识,我们是不能辨识的。于是,处在从未认识和即将遗忘的交界上,好像一切都和《大唐西域记》里的某个古地名没什么不同了。
- 阿耆尼國
- 屈支國
- 跋禄迦國
- 笯〈奴古反〉赤建國
- 赭時國
- 𢘥〈敷廢反〉捍國
- 窣〈蘇没反〉堵利瑟那國
- 颯秣建國
- 弭秣賀國
- 劫布呾那國
- 屈霜〈去聲〉你迦國
- 喝捍國
- 捕喝國
- 伐地國
- 貨利習彌伽國
- 羯〈去聲〉霜那國
- ……
边界、容纳和生命
某个课件中的某个式子会有对错,但对错的定义域是很小的。首先,生命的平凡不是错:人是目的而不是手段。
没有教学的教学环境也超出了对错的定义域。没有教学的教学环境本身是无意义的,但我们会因为这个无意义他者的存在,而转去寻找自己的意义,然后发现内心边界开始变化。
有时候我们的生活过得很平衡,有时候我们的生活过得很迷茫;很多时候我们会想,有些东西是可以不知道的,有些事是可以不想的,只有某些事才是我应做的。
有这样一个边界是对的,因为生命就是这么一回事。这个边界是用来定义自己的,而没有这边界就没有生命。不止是幻想的性质是排除非幻想,而且是生命的性质是排除非生命。
但边界不是生命的全部,称得上是生命的全部的是容纳。生命是芥子纳须弥,帕斯卡的芦苇,浑天仪里的每夜真实星辰。生命能在不同的选项中选择倾向于“游戏继续”而不是“游戏结束”的那一项:因为它能带来更丰富的可能性;因为这一项能最多地包容其他选项,生包容死,死却不包容生。
作为神经网络的自然性质,这种趋于丰富性的倾向是人的本能。是同一个看得见摸得着的本能过程让每个人长出两只眼睛、一个鼻子一张嘴,也让人追求知识、洞见力,追求心理需要的满足;它们有着一致的形成原理,只是存在于皮肤下的后者不如前者那么直观而已。
A. N. 怀特海:“微笑在脸上蔓延,因为脸适合微笑。”
“可以不想的”——人总会开始不再这么觉得的。因为边界是不可能一成不变的。为什么不愿意留在原地?不是不愿意,而是不能够。另一个角度,如果我想,时刻都有变化,就什么都有了;有一天我是否会暗想,如果能有什么不变的呢?
限制和具体
随着“是什么却不是一般的什么”的分辨,各种新概念就在头脑中和智慧一起产生了。
从本能的角度来说,智慧是人类对自然的爱。我们有时候只剩思念。
比如含两个命题变项 p 和 q、不含否定的合取范式有 p、q、p\wedge q、p\vee q,共 4 种。3 个变项的情形,可以这样列举:
std::vector<uint8_t> cases = { 0b10101010, 0b11001100, 0b11110000 };
bool done = false;
while (!done) {
done = true;
for (int i = 0; i < cases.size(); i++) {
for (int j = i + 1; j < cases.size(); j++) {
for (uint8_t pend : {cases[i] | cases[j], cases[i] & cases[j]}) {
if (find(cases.begin(), cases.end(), pend) == cases.end()) {
cases.push_back(pend);
done = false;
}
}
}
}
}
0 层公式 3 种,1 层 6 种,2 层 8 种,3 层 1 种。
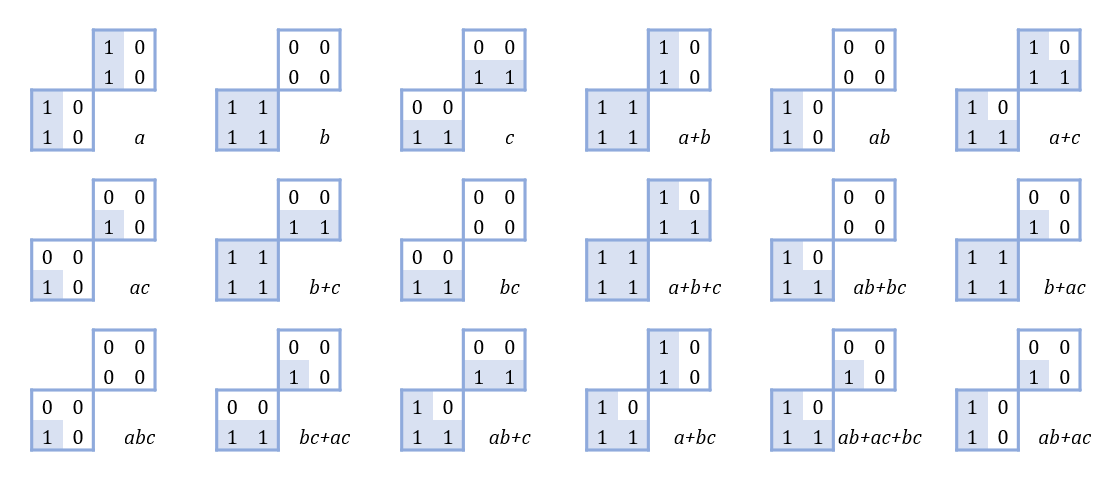
类似地可以得到:
| n | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| t | 1 | 4 | 18 | 166 | 7579 | 7828352 |
如果命题变项数为 7,大约需要富岳超算的 30000 节点时来得出结果。正好是这样一个算力规模:对每家中等规模的互联网公司拥有的计算资源来说,它都少得不值一提;但是一个普通人却难以企及。
而且以上只是列举而已。可以把这种不含否定的合取范式视为代数结构,归纳出它的性质吗?究竟有哪些学科研究过这样的问题呢?如果我们要做更进一步的研究,应该从哪里入手呢?很多时候我们看得见问题的样子,却找不到问题的位置。
意识是数学结构吗?就像历法是偏序集一样吗?
这种时候我们遇到的限制,是不够“黑格尔意义上的具体”的阻碍,或者说是思维的结构规模和可容纳信息量的限制。这里的“具体”更接近于“真实”的意思。比如,一个二元一次方程组就比一个一元一次方程更具体,因为在应用的时候我们知道前者能反应出比后者更多的现实。
但我们依然能认识这一点,能不再“只剩思念”,因为有超越自我的本能。
理解知觉
在“具体”的这个并非日常意义的定义下,很多日常会被称作抽象的事物,或者“大词”,实际上是非常具体的。比如战略思考是比战术思考更具体的,因为战略思考能认识更多的现实信息,所以能应对更多的变化。
但并不是能应对变化,定义了这种具体性;而是对于更广泛的、复杂的、不同的、真实的情形,都能给出确切的、唯一的、对应的做法,这定义了具体性。比如爱是非常具体的。
比如有的看似博学的理论,把所有部分都一条条列举出来,却给不出它们的内在相关性。这种基于收集而得到的、本轮均轮模型一样的理论,具体性寥寥无几,也自然不可能具有洞察力。
知觉性的思维是非常具体的。知觉是全脑以至全身直接参与的过程;而比如可以很容易地精确表达的简单计算,它不是知觉的思维而是严格逻辑思维,但它更像是在脑中运行的虚拟机而已,也就是说它的具体程度上限是更低的。或者说,表达是语法树的树梢表面,而语法树就长在神经网络上。所以,涉及具体程度很高的概念时,人们常见的做法是用比喻让知觉来为理解引路,用严谨性损失的增加来换具体性损失的减小,正如此句。
知觉是不稳定的、难以准确重现的,但也是可以认识、可以表达、可以最大程度地发挥人的认识力的。这是一个常被忽视的事实:一个只是作为朦胧的念头存在于脑中的想法,和一本已经写成严谨的学术文本的大部头著作,如果两者所包含的思维是完整相等的,那么两者之间的具体程度也不会有差异。而至今的多数时候,后者著作是不存在的,只有前者即各种各样的知觉结构,它们是时间的馈赠,而时间对每个人都是平等的。
标点符号用法的分析化过程,可以作为一个例子,用来了解对丰富的知觉性思维的忽视。古典文本中的符号,只是漂在流水一样延续的正文上的记号而已,用法类似于阿拉伯文的元音标记;而从电报出现的时代开始,发生了一个连续的、给标点符号赋予“字”的意义的过程。比如英式和美式的英文中,破折号(em dash)和前后单词之间是否需要留空格的区别,就是这一过程造成的。
每个单词的间距是均匀的,而标点附着在字母之间。
图源 德州大学数字图书馆。
釋德儀 明永樂 17 年(1419)印。
图源 中华古籍资源库。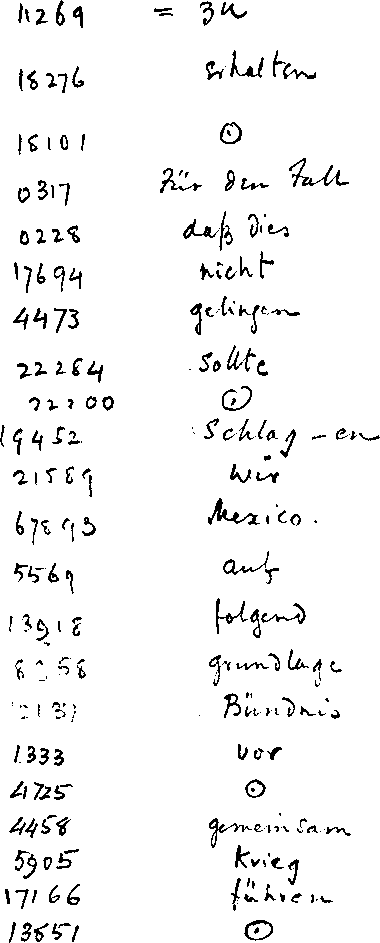
图源 美国国家档案馆。
知觉的图示
人的知觉世界本身就是因为“不是不愿意,而是不能够”而形成的。意识不处在做梦状态的每一刻,它的输入都来自于它自身之外。
有一个小小的启示:如果我要尊重他人,我就要预设每个人的心里都有一件珍视的东西;如果我要避免自己的认知受自己的蒙蔽,以至犯下傲慢之罪,那么我与每个具体的人交流的出发点,都应该建立在这样一个无条件承认之上:即对具体的交流对方内在珍视之物的意义的无条件承认。珍视之物是一个概念,指代了内心边界定义的整体知觉世界。
我们可以用这样一幅图示来说明人的知觉世界。左侧是趋于非生命的方向,右侧是趋于生命的方向。
chaos -> politics -> science -> state-of-the-
art -> -> -> -> -> -> -> -> -> -> -> -> -> -> fantasies
V (uncanny valley)
chaos(混沌)是自然世界的寻常事物,比如花草树木、山水石头等等。这里有个特别的例子是草履虫,如果我们去观察它,它就像水中一个会动的泡泡;当细胞膜破碎的一刻,它的生命也就结束了。
我们可以用液泡来形容草履虫,也可以同样地形容一番人的身体,把人比作包裹石灰石的浪花。如果看人体的每一个细胞,从脂质双分子层的细胞膜到透明的细胞质,细胞的绝大部分都是液体,剩余部分又充满了有机质,用浪花中微小的泡沫来比喻非常合理;用石灰石来形容绝大部分是碳酸钙的骨骼也非常贴切。
但是,尽管人的身体是非常类似于山、水、石头的自然造物,人本身是不属于 chaos 的。人认知中的自我在第一行右侧,uncanny valley(恐怖谷)的深谷之后的地方。从人的位置看去,chaos 有一个关键的临界点:对于属于 chaos 中的事物,“药”和“毒”两个概念之间的区别会被消解。
在这个临界点之后就进入了 uncanny valley,对人们来说这是一个接近自己但不属于自己的地方。它离人们自我认知的位置是如此之近,却又处在非生命的方向上,脱离了 chaos 的它体现出的这种微妙的异质性,会激发人的负面情绪本能,这个事实是无法避免的。实际上这里是人的负面情绪的唯一来源。
想避免受伤,总是不太简单。
因为它的存在,我们只能不问来路,这种问是一种跳崖。尽管随着去路继续走下去,有了新的来路,旧的来路也是会变得可问、重新被接纳的。
接下来的 politics(政治)是一个更广义的概念,包括社会意义上的强力机关,包括“横扫牛鬼蛇神”和“团结就是力量”,也包括人内心的某些没有严格道理、甚至不自洽的坚持。它只是筑在 uncanny valley 边上的一层矮矮的篱笆,尽职地让 uncanny valley 里的杀戮、精神污染一类的东西从人们认知的第一行上离开,去到看不见的第三行上。
science(科学)是所有可以精确描述的思维,它的特点是:如果被表述出来,进入别人的头脑的这种思维,可以和自己头脑中的这种思维保持完全一致。
state-of-the-art(艺术状态 / 顶级的)比 science 还更靠近生命的丰富性一些,它的特点是如果被表述出来,就会留有别人自己的补全空间。例如通过重复、延续和各种形式方法创作的音乐或诗歌,具有的补全空间是激发情绪;而设想一下篆书到草书的演进,就可以理解书法艺术具有的补全空间是激发形象感。
人的现实存在和更高程度的生命之间的界限就在 state-of-the-art 的内部。需要解释这里的“更高程度”的意思:对于生命的意义,有一种说法是把它视作一个无量概念。认为它就像地平线,我们能看得到它,并且会永远追着它跑,却永远到不了它。然而这是错的,实际上:我们确实能看得到生命的意义,这就是反过来取消掉地平线的意义,因为我们有了斯普特尼克。地平线是限制,而不是解放;而解放是仓颉、燧人氏、神农氏和无限的来者。
一个现实的例子是:例如一个能跨不同国家证券市场的数据、分析其关联的投资量化模型,其收益率就能做到高于数据来源只限于一个市场的模型。
所以,只要我们设想一位原始人山洞中的壁画作家,就很容易理解上文的“界限在 state-of-the-art 内部”的意思了,也可以理解从第一行到第二行的换行,这是一个非常自然的隐喻。
自我认知的位置会变化。所有的后退都只体现一种“无力”的扩大,而所有的前进都会体现一种“主动”。就像人长出五官不是因为有人刻意惩罚一样,前进后退不完全是因为人的奖惩,它们是自然的奖惩的结果。
换行是随着内心边界的变化持续存在的。在这个换行的位置上,一切意义都可以消解,因为一切意义都要重建。在第二行上,从 chaos 到 state-of-the-art 都要得到新的内省和接纳,来更高程度地实现 fantasies(幻想)。fantasies 就是花果山,是自在,是“在残骸和梦幻中选择了后者”的叙事。
不可避免地,第二行会穿过 uncanny valley。这里就存在着一种对未知的、处在自我之外的力量的畏惧,畏惧它损坏自己的一切。这种知觉结构是一种像《古明地恋的心跳大冒险》和 local58 频道一样的东西。它的存在抑制着换行,这是应该理解的。uncanny 是真的会伤人的。
但是只要我们达到了更高程度的生命,旧的 uncanny 退入了 chaos,它们就不值一提了。这就是我们工业革命以来的历史。
《恋跳》(“KKHTA”)和 local58 是其中的两个系列。 pid=95749793
明天
让这些文字去寻找它们的后续吧。
我们没有和历史一样的未来。而总是在冷暖变化中的人心,常像多变的水面。谁能许诺我们会迎来一个大道之行的时代,会迎来新的神农氏和仓颉、玄奘和鉴真呢?
可是我们并不需要这样的许诺。
就算宇宙会热寂,也许遥远遥远的未来的智慧生物也能造出一个新的宇宙呢?那不过是神明的大事。
明天,比永远多一天。
自然世界本身是没有教学法的,如果用人格来描述自然世界整体,它就是不可知论教学法。但人们却能从中学到完美能包容不完美,学到求知,学到“可言之理应尽言说”,还有“对于不可言说的东西,保持沉默”。
